Statistika
adalah ilmu yang mempelajari bagaimana merencanakan, mengumpulkan,
menganalisis, menginterpretasi, dan mempresentasikan data. Singkatnya,
statistika adalah ilmu yang berkenaan dengan data. Istilah 'statistika'
(bahasa Inggris: statistics) berbeda dengan 'statistik' (statistic).
Statistika merupakan ilmu yang berkenaan dengan data, sedang statistik
adalah data, informasi, atau hasil penerapan algoritma statistika pada
suatu data. Dari kumpulan data, statistika dapat digunakan untuk
menyimpulkan atau mendeskripsikan data; ini dinamakan statistika
deskriptif. Sebagian besar konsep dasar statistika mengasumsikan teori
probabilitas. Beberapa istilah statistika antara lain: populasi, sampel,
unit sampel, dan probabilitas.
Statistika
banyak diterapkan dalam berbagai disiplin ilmu, baik ilmu-ilmu alam
(misalnya astronomi dan biologi maupun ilmu-ilmu sosial (termasuk
sosiologi dan psikologi), maupun di bidang bisnis, ekonomi, dan
industri. Statistika juga digunakan dalam pemerintahan untuk berbagai
macam tujuan; sensus penduduk merupakan salah satu prosedur yang paling
dikenal. Aplikasi statistika lainnya yang sekarang popular adalah
prosedur jajak pendapat atau polling (misalnya dilakukan sebelum
pemilihan umum), serta jajak cepat (perhitungan cepat hasil pemilu) atau
quick count. Di bidang komputasi, statistika dapat pula diterapkan
dalam pengenalan pola maupun kecerdasan buatan.
Diagram Garis
Penyajian
data statistik dengan menggunakan diagram berbentuk garis lurus disebut
diagram garis lurus atau diagram garis. Diagram garis biasanya
digunakan untuk menyajikan data statistik yang diperoleh berdasarkan
pengamatan dari waktu ke waktu secara berurutan. Sumbu -X menunjukkan
waktu-waktu pengamatan, sedangkan sumbu Y menunjukkan nilai data
pengamatan untuk suatu waktu tertentu. Kumpulan waktu dan pengamatan
membentuk titik-titik pada bidang XY, selanjutnya kolom dari tiap dua
titik yang berdekatan tadi dihubungkan dengan garis lurus sehingga akan
diperoleh diagram garis atau grafik garis.
Diagram Lingkaran
Diagram
lingkaran adalah penyajian data statistik dengan menggunakan gambar yang
berbentuk lingkaran. Bagian-bagian dari daerah lingkaran menunjukkan
bagianbagian atau persen dari keseluruhan. Untuk membuat diagram
lingkaran, terlebih dahulu ditentukan besarnya persentase tiap objek
terhadap keseluruhan data dan besarnya sudut pusat sektor lingkaran.
Diagram Batang
Diagram
batang umumnya digunakan untuk menggambarkan perkembangan nilai suatu
objek penelitian dalam kurun waktu tertentu. Diagram batang menunjukkan
keterangan-keterangan dengan batangbatang tegak atau mendatar dan sama
lebar dengan batang-batang terpisah.
Contoh
soal-X menunjukkan waktu-waktu pengamatan, sedangkan sumbu Y menunjukkan
nilai data pengamatan untuk suatu waktu tertentu. Kumpulan waktu dan
pengamatan membentuk titik-titik pada bidang XY, selanjutnya kolom dari
tiap dua titik yang berdekatan tadi dihubungkan dengan garis lurus
sehingga akan diperoleh diagram garis atau grafik garis.
Grafik atau Diagram.
1. Penyajian Data dalam Bentuk Tabel
Misalkan,
hasil ulangan Bahasa Indonesia 37 siswa kelas XI SMA 3 disajikan dalam
tabel di samping. Penyajian data pada Tabel 1.1 dinamakan penyajian data
sederhana. Dari tabel 1.1, Anda dapat menentukan banyak siswa yang
mendapat nilai 9, yaitu sebanyak 7 orang. Berapa orang siswa yang
mendapat nilai 5? Nilai berapakah yang paling banyak diperoleh siswa?
Jika data hasil ulangan bahasa Indonesia itu disajikan dengan cara
mengelompokkan data nilai siswa, diperoleh tabel frekuensi berkelompok
seperti pada Tabel 1.2. Tabel 1.2 dinamakan Tabel Distribusi Frekuensi.
2. Penyajian Data dalam Bentuk Diagram
Kerapkali
data yang disajikan dalam bentuk tabel sulit untuk dipahami. Lain
halnya jika data tersebut disajikan dalam bentuk diagram maka Anda akan
dapat lebih cepat memahami data itu. Diagram adalah gambar yang
menyajikan data secara visual yang biasanya berasal dari tabel yang
telah dibuat. Meskipun demikian, diagram masih memiliki kelemahan, yaitu
pada umumnya diagram tidak dapat memberikan gambaran yang lebih detail.
a. Diagram Batang
Diagram
batang biasanya digunakan untuk menggambarkan data diskrit (data
cacahan). Diagram batang adalah bentuk penyajian data statistik dalam
bentuk batang yang dicatat dalam interval tertentu pada bidang
cartesius. Ada dua jenis diagram batang, yaitu
1) diagram batang vertikal, dan
2) diagram batang horizontal.
b. Diagram Garis
Pernahkah
Anda melihat grafik nilai tukar dolar terhadap rupiah atau pergerakan
saham di TV? Grafik yang seperti itu disebut diagram garis. Diagram
garis biasanya digunakan untuk menggambarkan data tentang m keadaan yang
berkesinambungan (sekumpulan data kontinu). Misalnya, jumlah penduduk
setiap tahun, perkembangan berat badan bayi setiap bulan, dan suhu badan
pasien setiap jam.Seperti halnya diagram batang, diagram garis pun
memerlukan sistem sumbu datar (horizontal) dan sumbu tegak (vertikal)
yang saling berpotongan tegak lurus. Sumbu mendatar biasanya menyatakan
jenis data, misalnya waktu dan berat
Adapun
sumbu tegaknya menyatakan frekuensi data. Langkah-langkah yang dilakukan
untuk membuat diagram garis adalah sebagai berikut.
1) Buatlah
suatu koordinat (berbentuk bilangan) dengan sumbu mendatar menunjukkan
waktu dan sumbu tegak menunjukkan data pengamatan.
2) Gambarlah titik koordinat yang menunjukkan data pengamatan pada waktu t.
3) Secara berurutan sesuai dengan waktu, hubungkan titiktitik koordinat tersebut dengan garis lurus.
c. Diagram Lingkaran
Untuk
mengetahui perbandingan suatu data terhadap keseluruhan, suatu data
lebih tepat disajikan dalam bentuk diagram lingkaran. Diagram lingkaran
adalah bentuk penyajian data statistika dalam bentuk lingkaran yang
dibagi menjadi beberapa juring lingkaran. Langkah-langkah untuk membuat
diagram lingkaran adalah sebagai berikut.
1. Buatlah sebuah lingkaran pada kertas.
2. Bagilah
lingkaran tersebut menjadi beberapa juring lingkaran untuk menggambarkan
kategori yang datanya telah diubah ke dalam derajat.
3. Tabel Distribusi Frekuensi, Frekuensi Relatif dan Kumulatif, Histogram, Poligon Frekuensi, dan Ogive
a. Tabel Distribusi Frekuensi
Data yang
berukuran besar (n > 30) lebih tepat disajikan dalam tabel distribusi
frekuensi, yaitu cara penyajian data yang datanya disusun dalam
kelas-kelas tertentu. Langkah-langkah penyusunan tabel distribusi
frekuensi adalah sebagai berikut.
• Langkah
ke-2 menentukan banyak interval (K) dengan rumus "Sturgess" yaitu: K= 1 +
3,3 log n dengan n adalah banyak data. Banyak kelas harus merupakan
bilangan bulat positif hasil pembulatan.
• Langkah ke-3 menentukan panjang interval kelas (I) dengan menggunakan rumus:
• Langkah
ke-4 menentukan batas-batas kelas. Data terkecil harus merupakan batas
bawah interval kelas pertama atau data terbesar adalah batas atas
interval kelas terakhir. • Langkah ke-5 memasukkan data ke dalam
kelas-kelas yang sesuai dan menentukan nilai frekuensi setiap kelas
dengan sistem turus. • Menuliskan turus-turus dalambilangan yang
bersesuaian dengan banyak turus.
b. Frekuensi Relatif dan Kumulatif
Frekuensi
yang dimiliki setiap kelas pada tabel distribusi frekuensi bersifat
mutlak. Adapun frekuensi relatif dari suatu data adalah dengan
membandingkan frekuensi pada interval kelas itu dengan banyak data
dinyatakan dalam persen. Contoh: interval frekuensi kelas adalah 20.
Total data seluruh interval kelas = 80 maka frekuensi relatif kelas ini
adalah
Frekuensi relatif dirumuskan sebagai berikut.
Frekuensi
kumulatif kelas ke-k adalah jumlah frekuensi pada kelas yang dimaksud
dengan frekuensi kelas-kelas sebelumnya. Ada dua macam frekuensi
kumulatif, yaitu
1) frekuensi kumulatif "kurang dari" ("kurang dari" diambil terhadap tepi atas kelas)
2) frekuensi kumulatif "lebih dari" ("lebih dari" diambil terhadap tepi bawah kelas).
c. Histogram dan Poligon Frekuensi
Histogram
merupakan diagram frekuensi bertangga yang bentuknya seperti diagram
batang. Batang yang berdekatan harus berimpit. Untuk pembuatan
histogram, pada setiap interval kelas diperlukan tepi-tepi kelas.
Tepi-tepi kelas ini digunakan unntuk menentukan titik tengah kelas yang
dapat ditulis sebagai berikut.
Poligon
frekuensi dapat dibuat dengan menghubungkan titik-titik tengah setiap
puncak persegipanjang dari histogram secara berurutan. Agar poligon
"tertutup" maka sebelum kelas paling bawah dan setelah kelas paling
atas, masing-masing ditambah satu kelas.
d. Ogive (Ogif)
Grafik yang
menunjukkan frekuensi kumulatif kurang dari atau frekuensi kumulatif
lebih dari dinamakan poligon kumulatif. Untuk populasi yang besar,
poligon mempunyai banyak ruas garis patah yang menyerupai kurva sehingga
poligon frekuensi kumulatif dibuat mulus, yang hasilnya disebut ogif.
Ada dua macam ogif, yaitu sebagai berikut.
a. Ogif dari frekuensi kumulatif kurang dari disebut ogif positif.
b. Ogif dari frekuensi kumulatif lebih dari disebut ogif negatif.
1. Rumus Rataan Hitung (Mean)
Rata-rata hitung dihitung dengan cara membagi jumlah nilai data dengan banyaknya data. Rata-rata hitung bisa juga disebut mean.
Rata-rata hitung dihitung dengan cara membagi jumlah nilai data dengan banyaknya data. Rata-rata hitung bisa juga disebut mean.
a) Rumus Rataan Hitung dari Data Tunggal
b) Rumus Rataan Hitung Untuk Data yang Disajikan Dalam Distribusi Frekuensi
Dengan : fixi = frekuensi untuk nilai xi yang bersesuaian
xi = data ke-i
c) Rumus Rataan Hitung Gabungan
2. Rumus Modus
a. Data yang belum dikelompokkan
Modus dari data yang belum dikelompokkan adalah ukuran yang memiliki frekuensi tertinggi. Modus dilambangkan mo.
b. Data yang telah dikelompokkan
b. Data yang telah dikelompokkan
Rumus Modus dari data yang telah dikelompokkan dihitung dengan rumus:
Dengan : Mo = Modus
L = Tepi bawah kelas yang memiliki frekuensi tertinggi (kelas modus) i = Interval kelas
b1 = Frekuensi kelas modus dikurangi frekuensi kelas interval terdekat sebelumnya
b2 = frekuensi kelas modus dikurangi frekuensi kelas interval terdekat sesudahnya
3. Rumus Median (Nilai Tengah)
a) Data yang belum dikelompokkan
Untuk mencari median, data harus dikelompokan terlebih dahulu dari yang terkecil sampai yang terbesar.
b) Data yang Dikelompokkan
Dengan : Qj = Kuartil ke-j
j = 1, 2, 3
i = Interval kelas
Lj = Tepi bawah kelas Qj
fk = Frekuensi kumulatif sebelum kelas Qj
f = Frekuensi kelas Qj
n = Banyak data
4. Rumus Jangkauan ( J )
Selisih antara nilai data terbesar dengan nilai data terkecil.
5. Rumus Simpangan Quartil (Qd)
6. Rumus Simpangan baku ( S )
7. Rumus Simpangan rata – rata (SR)
8. Rumus Ragam (R)

















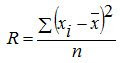

0 komentar:
Posting Komentar